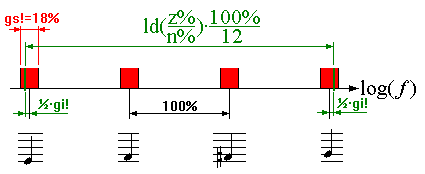
Chromatisches Tonleiter-Schema mit allen Grössen
Commodore spendierte dem Amiga einen mit 4 Tongeneratoren ausgestatteten
Soundchip, welchen Sie auch von AmigaBASIC aus nutzen können durch
Angabe des vierten, bei der MS-DOS-Welt nicht vorhandenen Parameters beim
SOUND-Befehl.
Mit SOUND können Sie gegenüber der MS-DOS-Welt recht
einfach und effektiv mehrstimmige Musik programmieren. Falls Sie wie
ich auch schon versuchten, ganze Partituren umzusetzen, sind Sie sicherlich
auch schon an die Grenzen gestossen, weil Sie bei nur 4 Stimmen ziemlich
rigoros Akkordnoten reduzieren mussten.
Der WAVE-Befehl erlaubt es Ihnen, über diese
systembedingten Grenzen hinauszugehen, und zwar ohne der Notwendigkeit einer
Maschinenspracheroutine. Beispiel eines einfachen Akkords:
' Klassisch programmierter Akkord SOUND WAIT SOUND 440, 14! SOUND 660, 14! SOUND RESUME
Dies ist die klassische Programmierung, welche Sie bestens kennen. Aber ihr
Nachteil ist bekanntlich die Tatsache, dass sie zwei Tongeneratoren
belegt. Und genau dies können wir vermeiden mit WAVE:
' Dasselbe mit nur einem Tongenerator Pi!=4!*ATN(1!) DIM Wa%(255) FOR i%=0 TO 255 w!=CSNG(i%)*Pi!/128! Wa%(i%)=CINT(INT(63.99!*(SIN(2!*w!)+SIN(3!*w!)))) NEXT i% WAVE 0,Wa% SOUND 220,14,255,0
Genau auf dieser Grundlage basieren die 8-stimmigen Stücke der Musiksammlung. Einige Erläuterungen dazu:
SOUND-Befehl rückkompensiert.Damit Sie nach Belieben zwei Noten auf diese Art und Weise kombinieren können, muss für jedes Frequenzverhältnis eine passende solche Wellenform gefunden werden. Wie Sie aber im Artikel über Tonprogrammierung entnehmen können, ist es ja aufgrund der temperierten Tonleiter und den damit verbundenen, irrationalen Frequenzverhältnissen gar nicht richtig möglich, exakte solche Wellenformen zu bilden, denn es muss ja immer eine ganze Anzahl Wellenperioden in der Wellenform erzeugt werden.
Wie im Artikel über Tonprogrammierung erwähnt interessiert sich unser menschliches Ohr nur für Frequenzverhältnisse, daher müssen wir geeignete Näherungsbrüche suchen, zu welchen dann diese Wellenformen erzeugt werden können.
gs!=18!:Th%=0 DIM wf%(3327),fk!(12),ft!(24)
Als Genauigkeit sollen die Töne maximal 18% eines Halbtonschrittes auseinanderliegen.
Umr!=ATN(1!)/32! FOR i%=0 TO 255 w!=CSNG(i%)*Umr! wf%(i%)=CINT(127!*SIN(w!)+25.4*(COS(2!*w!)+2*SIN(3!*w!))) NEXT i% fk!(0)=1!
Der einfachste Fall, beide Töne gleich, kann direkt berechnet werden. Um den Klang etwas interessanter zu machen, werden noch Oberschwingungen hineingemischt (sog. FM-Synthese).
PRINT "Bitte warten!"
FOR i%=1 TO 12
PRINT "*";
vt!=CSNG(i%)*LOG(2!)
gi!=1000000!
n%=0
WHILE gi!>gs!
n%=n%+1
z!=CSNG(n%)*EXP(vt!/12!)
z1%=CINT(INT(z!))
z2%=z1%+1
Zu jedem Frequenzverhältnis findet eine Bruchsuche statt. Dazu werden alle Nennerwerte durchgegangen und durch Auf- und Abrunden zwei Zählerwertvorschläge berechnet.
g1!=ABS(LOG(CSNG(z1%)/CSNG(n%))*12!-vt!)*100!/LOG(2!)
g2!=ABS(LOG(CSNG(z2%)/CSNG(n%))*12!-vt!)*100!/LOG(2!)
Hier wird die Abweichung als Prozentwert auf der chromatischen Tonleiterskala berechnet.
IF g1!<g2! THEN
gi!=g1!
z%=z1%
ELSE
gi!=g2!
z%=z2%
END IF
WEND
Der bessere »Kandidat« wird verwendet. Ist die geforderte Genauigkeit erreicht, so sind z% und n% das geeignete Zähler-/Nennerpaar.
Hinweis zum Experimentieren: Variieren Sie gs! und hören Sie sich dann jeweils das Musikstück
an. Bei entsprechend grossem Toleranzwert erhalten Sie zwar klarere Töne,
aber es tönt entsprechend wie ein verstimmtes Musikinstrument. Ein zu
genaues gs! ergibt dann teilweise solche
Frequenzverhältnisse, welche von der geringen Sampling-Auflösung von
WAVE nicht mehr sauber wiedergegeben werden können.
UmZ!=Umr!*CSNG(z%)
UmN!=Umr!*CSNG(n%)
FOR j=256*i% TO 256*i%+255
wz!=CSNG(j% AND 255)*UmZ!
wn!=CSNG(j% AND 255)*UmN!
wf(j%)=CINT(63.5*(SIN(wz!)+SIN(wn!))+12.7*(COS(2!*wz!)+COS(2!*wn!)+SIN(3!*wz!)+SIN(3!*wn!)))
NEXT j%
Hier wird die Wellenform mit dem gefundenen Zähler und Nenner erzeugt.
i1!=(CSNG(i%)/2!)*LOG(2!)-LOG(CSNG(z%)/CSNG(n%))*6! fk!(i%)=EXP(i1!/12!)/CSNG(n%) NEXT i%
Im anfänglichen Beispiel haben Sie die tiefer zu wählende Frequenz gesehen. Hier wird noch die zugehörige Umrechnungskonstante bezogen auf den tieferen Ton der beiden Noten berechnet. Und zwar erfolgt die Berechnung derart, dass der Bruchnäherungsfehler auf beide Noten gleich verteilt ist. Dies geschieht auch wiederum logarithmisch, d.h. nicht die Differenzen sind gleich, sondern der Fehlerfaktor.

Chromatisches Tonleiter-Schema mit allen Grössen
Das Toleranzfeld gs! verteilt sich symmetrisch bei jedem Halbton auf jeweils ±9% (rote Bereiche). Die Frequenz-Umrechnungskonstante fk!() wird so gewählt, dass die beiden grün dargestellten Abweichungen genau gleich gross sind, wenn man das ganze logarithmisch betrachtet. Dabei entspricht ein Halbtonschritt 100%.
FOR k=0 TO 1
IF St(2*j+k)=-2 THEN
n$="---"
ELSE
n$=MID$(Takt$,St(2*j+k),3)
END IF
IF n$="***" THEN
nc(k)=32767
ELSEIF n$="---" THEN
nc(k)=32766
ELSE
nc(k)=INSTR("c c#d d#e f f#g g#a b h ",LEFT$(n$,2))\2+12*VAL(RIGHT$(n$,1))
END IF
NEXT k
Das Notenpaar auf einem Tongenerator wird herausgelesen.
IF nc(1)<nc(0) THEN
SWAP nc(0),nc(1)
END IF
Die Grössenrelation muss stimmen, da e 4g 4 und g 4e 4 genau gleichwertig sind.
ELSEIF nc(0)<32766 AND nc(1)=32766 THEN
WPo(i,j)=1
f!(i,j)=440!*2!^(CSNG(nc(0)-57+Th)/12!)
Beim Einzelton (der andere Teilkanal hat gerade Pause) kann die normale Tonfrequenz verwendet werden.
ELSEIF nc(0)<32766 AND nc(1)<32766 THEN
WPo(i,j)=256*(nc(1)-nc(0))
f!(i,j)=440!*2!^(CSNG(nc(0)-57+Th)/12!)*fk!(nc(1)-nc(0))
Sonst muss mit dieser Hilfsfrequenz gearbeitet werden. Damit das Programm
also während des Abspielens nichts mehr berechnen muss, wird hier direkt
die fertige Frequenz für SOUND sowie die für diese
Doppelnote passende Wellenform ausgesucht und bereitgemacht.
ELSE
PRINT "Ungültige Zusammensetzung zweier Halbstimmen"
PRINT "in Position";i;j
END
END IF
NEXT j
Der ganze Trick hat natürlich auch seinen Preis, dass ein Notenpaar immer synchron pro Kanal gespielt sein muss. Dies ist aber bei vielen Musikstücken der Fall, weil ganze Akkorde gespielt werden.
PRINT "Stück wird gespielt..."
ta!=240!/Zaehlaufl!/Tempo!-.03
t!=TIMER+.5
SOUND RESUME
FOR i=0 TO gL-1
SOUND WAIT
FOR j=0 TO 3
IF t1!(i,j)<>0! THEN SOUND f1!(i,j),t1!(i,j),L(i)\(1-(Wp(i,j)=1)),j
NEXT
t!=t!+ta!
WHILE TIMER<t!:WEND
FOR j=0 TO 3
IF Wp(i,j)<>2 THEN WAVE j,wf(Wp(i,j)-(Wp(i,j)=1))
NEXT j
t!=t!+.03:WHILE TIMER<t!:WEND:SOUND RESUME
NEXT i
Beim Abspielen wird entsprechend die Wellenform laufend geändert. Das Ganze finden Sie in der Musiksammlung praktisch angewendet, so dass ich Sie für die übrigen Details der Ausprogrammierung dorthin verweisen möchte.